This article is intended to be a "application-oriented tutorial" for Tensorflow by using Tensorflow to implement a linear support vector machine (LinearSVM). Although using mnist as an introductory tutorial project is almost a matter of convention, I always feel like copying such a thing and there is some water in the column... so I still handwritten a LinearSVM ( σ'ω') σ
Before implementing, let's briefly introduce the LinearSVM algorithm (see here for details):
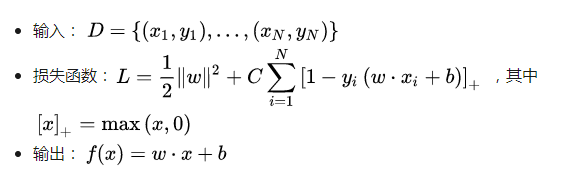
And introduce some ideas of Tensorflow:
The core of Tensorflow is that it can build a "Graph", all we need to do is add elements to this Graph.
The basic elements are as follows: constant, variable (variable) and non-trainable (Variable (trainable=False))
Since machine learning algorithms can often be transformed into minimizing loss functions, Tensorflow takes advantage of this and encapsulates the “minimize loss†step. Specifically, you only need to express the loss in the Graph and then call the corresponding function to complete the update of all trainable variables.
The third point we will explain when implementing LinearSVM, here will focus on the second point. First, let's look at how to define three basic elements and the corresponding addition, subtraction, multiplication, and division. (It is worth mentioning that in Tensorflow, we often call the Tensorflow variable in the Graph "Tensor", so Tensorflow Can be understood as "Tensor's flow") (Note: Tensor is called tensor, mathematically quite a bit of something; but personally think that if you are not doing research, you can completely ignore the mathematical connotation, treat it as High-dimensional arrays are good ( σ'ω') σ):
Import tensorflow as tf
# Define constants and define the data type as a type of tf.float32 that can perform GPU calculations
x = tf.constant(1, dtype=tf.float32)
# Define a trainable variable
y = tf.Variable(2, dtype=tf.float32)
# Define untrainable variables
z = tf.Variable(3, dtype=tf.float32, trainable=False)
X_add_y = x + y
Y_sub_z = y – z
X_times_z = x * z
Z_div_x = z / x
In addition, Tensorflow basically supports all the methods in Numpy, but the interface it leaves us may be slightly different. Take the "summation" operation as an example:
# Initializing Tensor with Numpy Array
x = tf.constant(np.array([[1, 2], [3, 4]]))
#滕sorflow corresponds to the method of np.sum
Axis0 = tf.reduce_sum(x, axis=0) # will get a Tensor with a value of [ 4 6 ]
Axis1 = tf.reduce_sum(x, axis=1) # will get a Tensor with a value of [ 3 7 ]
More methods of operation can be found here (https://zhuanlan.zhihu.com/p/26657869)
Last but not least, in order to "extract" the value of Tensor in the Graph, we need to define a Session to do the corresponding work. You can understand the relationship between Graph and Session in this way. (Note: This understanding may be wrong! If I am really arguing, welcome the audience to point out (σ'ω') σ):
Defined in Graph is a set of "operation rules"
Session will "start" this set of rules defined by Graph, and during the startup process, Session may do three more things:
Extract the desired intermediate result from the algorithm
Update all trainable variables (if the starting algorithm includes the "Update Parameters" step)
Give some "placeholders" in the "Operational Rules" to specific values
The relevant descriptions of "update parameters" and "placeholders" will be described later. Here we only explain what "extract intermediate results" means. For example, there is such a set of arithmetic rules in Graph: and I only want the result of the operation of y after the operation rule is started. The code for this requirement is implemented as follows:
x = tf.constant(1)
y = x + 1
z = y + 1
Print(tf.Session().run(y)) # will output 2
If I want to get the results of y and z at the same time, just change the 4th line to the following code:
Print(tf.Session().run([y, z])) # will output [2, 3]
Finally, I want to point out a very easy place to make mistakes: when we use Variable, we must first call the initialized method before we can use the Session to extract the corresponding value from the Graph. For example, the following code will report an error:
x = tf.Variable(1)
Print(tf.Session().run(x)) # Report error!
Should be changed to:
x = tf.Variable(1)
With tf.Session().as_default() as sess:
Sess.run(tf.global_variables_initializer())
Print(sess.run(x))
The role of tf.global_variables_initializer() can be directly known by its name: Initialize all Variables
The next step is the implementation of LinearSVM. From the previous discussion, the key is to express the form of the loss function (using the ClassifierBase (https://link.zhihu.com/?target=https%3A//github.com) /carefree0910/MachineLearning/blob/master/Util/Bases.py%23L196); For the sake of brevity, we set C=1):
Import tensorflow as tf
From Util.Bases import ClassifierBase
Class TFLinearSVM(ClassifierBase):
Def __init__(self):
Super(TFLinearSVM, self).__init__()
Self._w = self._b = None
# Use the self._sess property to store a Session for easy invocation
Self._sess = tf.Session()
Def fit(self, x, y, sample_weight=None, lr=0.001, epoch=10 ** 4, tol=1e-3):
# Convert sample_weight (sample weight) to constant Tensor
If sample_weight is None:
Sample_weight = tf.constant(
Np.ones(len(y)), dtype=tf.float32, name="sample_weight")
Else:
Sample_weight = tf.constant(
Np.array(sample_weight) * len(y), dtype=tf.float32, name="sample_weight")
# Convert input data to constant Tensor
x, y = tf.constant(x, dtype=tf.float32), tf.constant(y, dtype=tf.float32)
# Define w and b that need training as trainable Variable
Self._w = tf.Variable(np.zeros(x.shape[1]), dtype=tf.float32, name="w")
Self._b = tf.Variable(0., dtype=tf.float32, name="b")
# ========== The next steps are important! ! ! ==========
# Call the corresponding method to get the current model prediction value
Y_pred = self.predict(x, True, False)
# Calculate the total loss using the corresponding function:
#cost = ∑_(i=1)^N maxâ¡(1-y_iâ‹…(wâ‹…x_i+b),0)+1/2 + 0.5 * ‖w‖^2
Cost = tf.reduce_sum(tf.maximum(
1 - y * y_pred, 0) * sample_weight) + tf.nn.l2_loss(self._w)
# Define the "Update Parameters" step with the Tensorflow encapsulated optimizer
# This step will call the corresponding algorithm to update the parameters for the purpose of reducing the total loss described above.
Train_step = tf.train.AdamOptimizer(learning_rate=lr).minimize(cost)
# Initialize all Variables
Self._sess.run(tf.global_variables_initializer())
#Continuously call the "update parameters" step; if the period finds that the error is less than the threshold, it will terminate the iteration early.
For _ in range(epoch):
# This is a relatively lazy way of writing, the cost will not be accurate
If self._sess.run([cost, train_step])[0] < tol:
Break
Then we need to define the method to get the predicted value of the model - self.predict:
Def predict(self, x, get_raw_results=False, out_of_sess=True):
# Calculate the prediction vector using the reduce_sum method
Rs = tf.reduce_sum(self._w * x, axis=1) + self._b
If not get_raw_results:
Rs = tf.sign(rs)
# If the out_of_sess parameter is True, use Session to calculate the specific value.
If out_of_sess:
Rs = self._sess.run(rs)
# Otherwise, return Tensor directly
Return rs
The reason for using an out_of_sess parameter to control the output is as follows:
Tensorflow does not need to calculate the specific values ​​when performing Graph operations internally. It is better to use the original Tensor for calculations.
When the model is trained, what we hope to get in the test phase is of course the specific value instead of Tensor. At this point, we need Session to help us extract the intermediate results.
The above is the complete implementation of LinearSVM, you can see it is quite simple
Here is a special point: the process of extracting intermediate results by using Session is not without loss; in fact, when the calculation of Graph operation itself is not large, the overhead caused by opening and closing Session will occupy the overall cost. most. Therefore, when we write the Tensorflow program, we must take care to avoid opening the Session at will because of the convenience of coveting.
At the end of this article, let's take a look at the application of the Placeholder in Tensorflow. Although the current implementation of LinearSVM can be used, there are hidden dangers in memory. In order to solve this hidden danger, a common practice is to divide the batch training, which will cause the data of the "update parameter" step to be accepted every time is "unfixed" data - a small batch of the original data. In order to describe this "unfixed" data, we need to use the "Placeholder" in Tensorflow, which is very intuitive to use:
# Define a matrix with data type tf.float32, "long" unknown, and "wide" 2.
Placeholder x = tf.placeholder(tf.float32, [None, 2])
# Define a numpy array: [ [ 1 2 ], [ 3 4 ], [ 5 6 ] ]
y = np.array([[1, 2], [3, 4], [5, 6]])
# Define x + 1 corresponding Tensor
z = x + 1
# Use Session and its feed_dict parameter, assign the value of y to x, and output the value of z print(tf.Session().run(z, feed_dict={x: y}))
# will output [ [ 2 3 ], [ 4 5 ], [ 6 7 ] ]
So the implementation steps of the Batch operation are very clear:
Define all x, y involved in calculating the loss as a placeholder
Each training, with a feed_dict parameter, a small batch of the original data is given to x, y
There are many other interesting application methods for placeholders. Their ideas are all the same: to define undetermined information in the form of a Placeholder, and to assign specific values ​​when it is actually called.
In fact, Placeholder is used in almost all Tensorflow models. Although the TFLinearSVM we implemented above is not used, it is because of this, it is a huge flaw (for example, if you repeatedly call the predict method whose parameter out_of_sess is True in the same piece of code, you will find that it is getting faster. The slower the audience, the spectators can think about why this is ( σ'ω') σ)
The above is a brief tutorial of Tensorflow. Although I wrote it with the heart of “I can understand it even if I have never used Tensorflowâ€, there may still be some places that are not detailed enough; if it is, I would like to point out ( Σ'ω')σ
Blue light filter-using blue light filter technology can eliminate blue light on the phone screen, thereby reducing eye fatigue and fatigue. And keep your eyes healthy and avoid staring at the screen.
Ultra-transparent and protective Ultra-high-quality Ultra HD provides you with clear viewing effects. Let you fully enjoy the super retina display of the screen.
Evacuation Waterproof and Waterproof-The hydrophobic and loose oil transparent layer is used as the final coating to protect screen fingerprints, liquid residues and other stains, keeping your phone in its original condition all day long.
The 0.14mm high-sensitivity touch Ultra-Thin Protective Film can provide real touch and high sensitivity, ensuring that the original high-response touch is not disturbed.
If you want to know more about Anti-Blue Light Screen Protector products, please click the product details to view the parameters, models, pictures, prices and other information about Anti-Blue Light Screen Protector.
Whether you are a group or an individual, we will try our best to provide you with accurate and comprehensive information about the Anti-Blue Light Screen Protector!
Anti-blue Screen Protector, Anti-blue Light Protective Film, Anti-blue Light Screen Protector,Anti Blue Light Screen Protector,Blue Light Blocking Screen Protector
Shenzhen Jianjiantong Technology Co., Ltd. , https://www.mct-sz.com