Improved Hybrid Genetic Algorithm for Distribution Network Reconfiguration
In this paper, an improved hybrid genetic algorithm based distribution network reconstruction algorithm is proposed. In the algorithm, the integer numbered sequence of the operable switch branches is used to represent the chromosomes, and the corresponding mapping of the chromosomes is mapped by the decoder design. The radial network structure avoids the situation of infeasible solutions and greatly improves the computational efficiency of the algorithm. At the same time, the local optimization operator is introduced into the algorithm, which improves the local optimization performance of the algorithm. The results of the example show that the algorithm is efficient and feasible.
Key word network reconstruction; genetic algorithm; local optimization algorithm
A refined hybrid geneTIc algorithm for
distribuTIon network reconfiguraTIon
ZHENG Xin1, YANG Li-xi1, CTTse2
(1. College of Electrical Engineering, ZhengZhou University,
ZhengZhou, 450002, China;
2.The Hong Kong Polytechnic University, Electric Engineering
Department,China)
In the algorithm the "the integer permutation" encoding is adopted with each integer representing one controllable switch. A decoder is designed to decide the final network configuration A local search operator is combined with the genetic algorithm which improve the local optimal capability of the algorithm. The computational result on a tested system demonstrate the algorithm is feasible and efficient.
Key words: Network reconfiguration; Hybrid genetic algorithm; Local search algorithm;
1 Introduction The problem of distribution network reconstruction based on minimum network loss is a typical nonlinear and multi-constrained integer combination optimization problem. The radial structure and weak ring network characteristics of distribution network are the preconditions for its reconstruction. Based on the graph theory, the structure of the distribution network can be described by the graph G(N, B), N represents the set of power nodes and load nodes, B represents the set of feeder segments, and the radial structure of the distribution network is from multiple trees of the graph. The composition, T={t1t2t3t4...tn, l1l2...lm}, wherein the tree branch t is a power supply branch, and the branch l is a contact branch. Thus, the problem of distribution network reconstruction can be described as finding a tree structure in the figure that minimizes the total network loss and satisfies the operational constraints. A large distribution network contains many nodes and branches, so the number of combinations of support trees in the figure is extremely large. If all trees are exhausted, the algorithm will be very inefficient.
Genetic algorithm has the advantages of global convergence, no micro-differentiability, and good robustness. It is especially suitable for solving combinatorial optimization problems. In addition, unlike the blind undirected search by the general random search method, the genetic algorithm performs an efficient and directed global search, which can gradually approximate and converge to the global optimal solution. Therefore, genetic algorithms are more and more widely used in distribution network reconstruction.
However, there are two important defects in the genetic algorithm for solving nonlinear combination optimization problems such as distribution network reconstruction. First, the high-quality gene structure of the father has little effect on the offspring. The conventional genetic algorithm uses a fairly slow convergence rate. Second, distribution network reconfiguration is a strong constraint problem. For current, voltage and other constraints, the penalty factor can be used to constrain, but the combination of ring network and island can not be evaluated by a suitable evaluation function. Literature [1]-[4] proposed different coding, hybridization and mutation operator design methods, although the efficiency of the algorithm is improved to a certain extent, but these algorithms based on binary coding method inevitably appear in the generation of the next generation. A large number of infeasible solutions. In these documents, there are two methods for dealing with infeasible solutions. One is to delete, and the other is to add the feasible solution to the new generation. The other method is to repair, and the network structure of the infeasible solution is solved by opening the switch and closing. The switch eliminates islands, making the infeasible solution a feasible solution. Although these two methods are theoretically feasible, they are only suitable for the case where a small number of infeasible solutions occur in each generation. In a complex, multi-ring distribution network, these algorithms will generate a large number of infeasible solutions in each generation. It takes a lot of time to judge whether the solution is feasible, and it is also very important to add new feasible solutions and repair infeasible solutions. Difficult and time consuming, increasing the complexity of the algorithm. At the same time, due to a large number of repairs and supplements of new individuals, the offspring cannot maintain the similarity with the parents. The high-quality gene structure in the father is completely destroyed in the offspring, and the algorithm may eventually become a blind random search and converge. The speed is slow, and even the phenomenon that it cannot converge, the meaning of the genetic algorithm is lost.
In this paper, an improved hybrid genetic algorithm is proposed. The local optimization operator is added to the conventional genetic algorithm to improve the local optimization performance of the algorithm. At the same time, the design method combining the encoder and the decoder completely avoids the infeasibility. The problem of solution further improves the search efficiency of the genetic algorithm, thereby accelerating the convergence speed of the genetic algorithm.
2 Mathematical model of distribution network reconstruction The purpose of network reconstruction is to minimize the network loss of the system under the premise of satisfying the operational constraints. Therefore, the objective function of the distribution network reconstruction can be expressed as: 
Where: Ie is the current of branch e, Re is the resistance of branch e, Ke is the switching state of the branch, 1 means that the branch switch is in the closed state, 0 means the branch switch is in the off state; (2) represents The branch current overload constraint, Iemax represents the upper limit of the branch current; (3) represents the node voltage constraint, Vimin and Vimax respectively represent the upper and lower limits of the node voltage, and (4) represents the radial network and does not appear the island topology constraint. . In this paper, the power flow algorithm of the distribution network is solved by the power flow algorithm which is pushed forward, and the constraint condition is used for verification.
3 Improvement of genetic algorithm in network reconstruction
3. 1 Coding and Decoding Strategy Coding design is how to use a chromosome to represent a unique distribution network structure; this article assigns all operable switch branches in the distribution network to integer numbers, and the chromosomes are all these branches. The random arrangement of the road numbers, the same branch number is not allowed in the chromosome, and the length of the chromosome is the number of operable switch branches. For example, a 16-node distribution system, 16 branches are numbered from 1 to 16, and one of the chromosomes can be expressed as:
[1 2 3 5 6 7 8 9 10 12 14 15 16 4 11 13]
For genetic algorithms, only strings of different order are randomly generated. In order for the string to represent an effective network topology, this requires the implementation of a decoder. The goal of the decoder is how to construct a unique support tree based on the coding of the chromosome.
In the design of the decoder, the construction method of the tree is avoided. At the beginning of the graph, only the nodes have no edges, and the set of tree branches and branches are empty. The branches are arranged from left to right according to the branch number in the chromosome. In order, select an edge corresponding to the branch number to join the graph; if the edge in the graph does not form a loop, it is placed in the tree branch set as a tree branch, otherwise it is added as a branch into the connected branch, and the process is repeated. Until it can't be done; this will eventually form a tree form, the tree branch is the closed branch, and the branch is the open contact branch. It can be seen that in the process of avoiding the circle generation tree, the edge added first in a weak ring will become a tree branch, and the last added edge will only form a ring because it will form a ring, so the order of joining the edges is different. Different trees may be different, and by this method each chromosome must correspond to only one distribution network with a single tree structure. Although the tree corresponding to different chromosomes may be the same, if the tree above is expressed as a chromosome, the order of arbitrarily changing the branches of the tree and the order of arbitrarily changing the branches are the same according to the tree generated by the avoidance method. However, we can reduce the probability of occurrence of equivalent chromosomes through continuous large-scale cross-conversion when generating the initial generation. In the examples in this paper, there are only a few chances for equivalent or identical chromosomes in each generation through specific crossover and mutation methods. Because of the method of constructing the support tree through the decoder, the corresponding natural solution is a feasible solution, so there is no need to judge whether the network structure conforms to the network topology constraint, and various processing steps for the infeasible solution are omitted. , greatly improve the quality of understanding and the efficiency of the algorithm, and accelerate the convergence of understanding.
3.2 The crossover operator design is based on the sequential coding of the construction support tree. If a simple one-point or multi-point crossover strategy is adopted, it is inevitable to generate infeasible chromosomes with great probability. Therefore, this paper adopts a crossover method similar to the partial matching crossover method. as follows:
(1) randomly select a mating area in the string, such as two parent strings and mating areas selected as:
A=12|3456|789 B=98|7654|321
(2) Add the mating area of ​​B to the front or the back of A, and the mating area of ​​A to the front or back of B to get:
A'=7654 B'=3456
(3) After the self-mating area in A' and B', the same city code as the mating area is deleted in turn, and the final two sub-strings are obtained:
A′′=765412389 B′′=345698721
Compared with other methods, this method can still produce a certain degree of variation effect under the same conditions of the two parents, which has a certain effect on maintaining certain diversified characteristics in the group. The experiment also shows good results. .
3.3 Mutation In order to maintain the diversity within the group, this paper adopts the variation technique of random continuous multiple swapping, which makes the feasible solution have a large change in order to suppress the possible assimilation in the cross.
The so-called random swap variation is to randomly select two points in the string and exchange their codes. For example, for string A:
A=12|3456|789
If the randomly generated switching points are 2 and 7, the second and seventh points in the string A will be swapped. After the swapping, the string A becomes:
A'=17|3456|289
Since after a swap, A' may still be represented by the same network structure as A, so this paper adopts multiple consecutive swap operations to enhance the effect of variation.
3.4 Update This paper uses the intergenerational update method to control the percentage of individuals in each generation group being updated by generational G. Among the N individuals in t generation, there are (1-G). N individuals with the highest fitness are selected to be completely copied to In the t+1 generation, only N*G new individuals are generated per generation. The intergenerational update method provides a condition for the genetic algorithm to use the historical information in the optimization process, and accelerates the convergence process of the genetic algorithm. However, the contemporary ditch may cause premature convergence of the genetic algorithm, and G generally takes 0.3. 1, this article takes 0. 8.
3.5 Fitness function Since genetic algorithm is a random search algorithm that is unconstrained in a given solution space, it is necessary to construct an accurate fitness function to guide the search direction of the genetic algorithm to approach the optimal solution. The fitness function in this paper consists of an objective function and a penalty function, defined as follows: 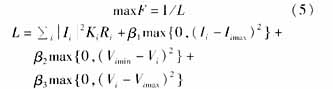
Among them: B1, B2, B3 are punishment factors, usually take a larger number to increase the penalty.
To calculate the fitness of an individual, it is necessary to decode the individual with a decoder, find the corresponding network structure, and then call the power flow calculation program to calculate the node voltage and the branch current into the formula (5) to calculate the fitness value of the individual. . When an individual violates the current and voltage constraints, because the penalty factor is relatively large, the fitness value will be very low, so it is easy to be eliminated in the evolution process.
4 Hybrid strategy of genetic algorithm and local optimization algorithm In the basic genetic algorithm, there are shortcomings of poor local search ability and slow convergence. If a suitable neighborhood-based local search mechanism is added to the genetic algorithm framework, and the genetic algorithm is combined with the traditional problem-based knowledge-based heuristic search technology to form a hybrid genetic algorithm combining global and local search, It is guaranteed that in each generation of population evolution, the solutions of the algorithm are local optimal solutions, and then the optimal solution is selected from the local optimal solutions through competition.
In this paper, we perform successive “multiple-forward interpolation†operations on the cross- and mutated chromosomes to find the best advantage of the local solution space where the chromosome corresponding solution is located. The chromosome is first decoded by the decoder into the form of the supporting tree T = {t1t2t3t4...tn, l1l2...lm}. In fact, the ordering in the tree branch set and the change of the order of the rows in the set of branches do not affect the structure of the distribution network, that is, the fitness does not change, only when the branch is connected with other trees in the ring. The branch exchange occurs, that is, the branch exchange occurs, and the network structure is affected. The pre-injection method is to insert the branch into the tree branch area, for example, to insert the branch l1 in the combination T forward. To the front of the tree branch t4, the combination of T becomes the form of {t1t2t3l1t4...tn, l2...lm}, which will become a tree branch due to the first addition, and the last tree branch in the same ring will change. Into the branch, thus achieving the branch exchange.
The "joint front insertion" used in this paper is a mountain climbing behavior (towards the direction of improvement) and a plurality of "pre-insertion" operations. If "pre-insertion" increases the fitness of the string, the operation is performed, and so on. Until it can no longer be inserted, the final combination will be replaced by the original chromosome. This operation actually improves the given string to its local pole, and this local hill climbing ability combined with the global search ability of the basic genetic algorithm shows good results in the experiment. As shown in Figure 1, the algorithm uses a local optimization operator to repair new individuals generated by hybridization and mutation, bringing it to the local best. In Fig. 1, the parental individual X and the individual Y produce the progeny individual Z', and the final individual Z is produced by local optimization.

5 Hybrid genetic algorithm flow of distribution network reconstruction After given the distribution network and data, the steps to apply the algorithm to solve the optimal operation scheme are as follows:
a. The algorithm first reads the original data for initialization, and sets the maximum evolutionary algebra of the genetic algorithm, population size N, generation G, chromosome length, hybrid probability, mutation probability and other parameters.
b. Using the branch integer coding method to randomly generate the first generation of the initial population as a parent. The individuals in the initial group are decoded, and the power flow calculation program is called to calculate the individual fitness and the average fitness of the group.
c. Based on the gambling wheel selection mechanism, the individuals with higher fitness are selected from the confession to perform cross operations, and a new generation of individuals is generated.
d. Perform mutation operations on the offspring.
e. Perform “continuous insertion and insertion†operations on the offspring individuals to further improve the individual.
f. Repeat steps c, d, e until the number of progeny individuals reaches N*G.
g. Perform an intergenerational update operation, copying N*(1-G) individuals with the highest fitness from the parent to the children.
h. Calculate the individual fitness of the offspring and the average fitness of the group, and use the offspring as the father of the next round of evolution.
i. When the algorithm reaches the preset maximum evolution algebra, the algorithm will end and output the network scheme corresponding to the individual with the highest fitness. Otherwise go to step c and continue the evolution.
6 Example analysis The example of this paper uses a 33-node, 5 tie switch distribution network test system [4], as shown in Figure 2.
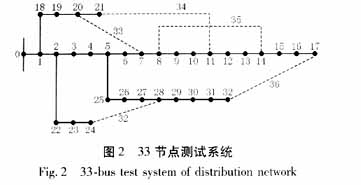
The five normally open contact switches are located on the branches 7-20, 11-21, 8-14, 17-32, 24-28. It is assumed that all the branches are equipped with segment switches. According to the coding method in the article, the power supply is used. The path does not participate in the reconstruction, is always closed, does not participate in the coding, so the length of the chromosome is 35, the population size is taken as 50, the crossover probability is taken as 0. 6, the probability of variation is taken as 0.01. After the operation program, the optimal reconstruction scheme is to close the segment switches on branches 7-20, 11-21, 8-14, 17-32, and disconnect 6~7,8-9,13~14,31 Section switch on ~32. Table 1 gives the results of the calculations and compares them with the results of the algorithm calculations in Document 4.
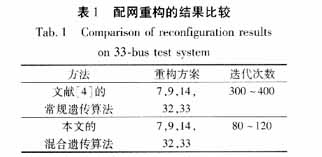
Compared with the algorithms described in [1]-[4], the convergence performance of this algorithm is greatly improved. Using the binary coding-based genetic algorithm in the literature, it is often necessary to carry out more than 300 generations of convergence in the same example. The algorithm is used to find the optimal individual in more than 40 generations, and the average fitness gradually becomes around 100 generations. Convergence is optimal, and compared with the literature [1]-[2], the computational efficiency of each generation is also greatly improved.
7 Conclusion When genetic algorithm is used to solve the large-scale combinatorial optimization problem in distribution network reconstruction, this paper uses branch integer coding method to realize gene coding and decoder design method based on constructive support tree method, which avoids generating infeasible solution. The situation reduces the invalid search of the algorithm and improves the computational efficiency. At the same time, the local optimization algorithm based on graph theory is proposed, which is added to the algorithm as a local optimization operator, which improves the local optimization performance of the algorithm and accelerates the convergence speed of the algorithm. The results of the example show that this method is feasible and effective.
15.6 inch Laptop is one of the most important sizes on the market, more than 85% clients choose this size for business, teachers, middle or high school students, university students projects. 15.6 inch Gaming Laptop is ranking the first level of custom laptop, you can see i5 15.6 inch laptop, intel celeron n5095 Cheap 15.6 Inch Laptop, i7 11th 15.6 Inch Laptop In cm, etc.
15inch gaming Laptop with 11th Gen Intel Core i5-1135G7 processor ( up to 4.2GHZ, 4core, 8threads, 8MB caches) or 15.6 inch i7 1165G7 8 512gb Solid State Drive laptop ( up to 4.7GHZ, 4core, 8threads, 12MB Caches) should attractive your eyes when choose a competitive and hot gaming laptop.
Of course, other parameters levels, like 14 inch n4020 64gb laptop for online classes, 10.1 Inch Laptop equipped with 64gb rom, android 11 or windows 10 , or 11 Inch Windows Laptop in metal with 360 rotating, celeron quad core cpu, etc.
Except, 8 inch Android Tablet, Mini PC host, All In One Desktop also available here. So just share your idea about what you exactly need, then we do following for you.
15.6 Inch Laptop,15.6 Inch Gaming Laptop,15.6 Inch Laptop In Cm,I5 15.6 Inch Laptop,Cheap 15.6 Inch Laptop
Henan Shuyi Electronics Co., Ltd. , https://www.shuyioemelectronics.com