A linear system is a system that satisfies both superposition and uniformity (also known as secondary). The so-called superposition means that when several input signals act on the system together, the total output is equal to the sum of the outputs produced when each input acts alone; the uniformity means that when the input signal is increased several times, the output is also increased accordingly. The same multiple. For linear continuous control systems, linear differential equations can be used to represent them. A system that does not satisfy the superposition and uniformity is a nonlinear system.
Since linear systems are easier to handle, many times the system is idealized or reduced to a linear system. Linear systems are often used in automatic control theory, signal processing, and telecommunications. The propagation of wireless communication signals in the medium can be simulated with a linear system.
The function of the linear system is expressed as

Figure:
If you look at the system state space expression, the most obvious difference between a linear system and a nonlinear system is that the linear system follows the superposition principle, while the nonlinear system does not.
The so-called superposition principle is an example:
f(x)=2x,f(y)=2y,f(x+y)=2(x+y)=2x+2y=f(x)+f(y)
To give a counterexample:
f(x)=2x^2,f(y)=2y^2,f(x)+f(y)=2(x^2+y^2), but f(x+y)=2(x +y)^2, the two obviously do not wait.
In other words, there are only one term of the state variable in the expression of the linear system, and there are no higher-order, trigonometric, and constant terms, as long as any nonlinear link is a nonlinear system.
Example of judging a linear systemIs it judged whether the system corresponding to the differential equation described below is a linear system?

analysis:
1) Uniformity
Let the signal e(t) act on the system and the response is r(t). When the excitation Ae(t) acts on the system, multiply the two sides of the equation by A according to the differential equation describing the system.
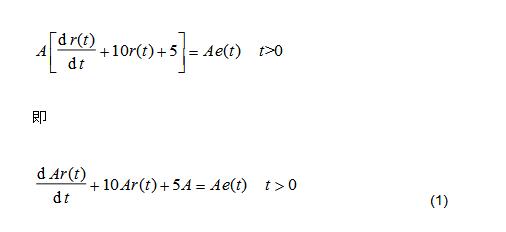
This is the result of the system and then linear operation.
The following is a discussion of the first linear operation, and then the results of the system. Obviously the stimulus after the linear operation is Ae(t). And if the system has uniformity, according to the differential equation describing the system, the result should be
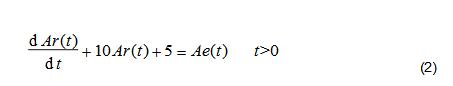
It is obvious that the formula (1) is not equal to the formula (2), that is, the system does not satisfy the uniformity.
2) Superposition
Assume that the two excitations are e1(t) and e2(t), respectively, and their corresponding responses are r1(t) and r2(t), respectively. According to the differential equation describing the system, the following relationship holds.

This is the result of the system and then linear operation.
The following is a discussion of the first linear operation, and then the results of the system. Obviously the excitation after the linear operation is e1(t)+e2(t). And if the system satisfies the superposition, according to the differential equation describing the system, the result should be
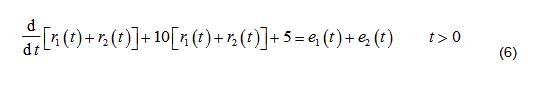
Obviously, equation (5) is not equal to equation (6), that is, the system does not satisfy the superposition.
It is known from the conclusions in 1) and 2) that the system does not satisfy the uniformity or the superposition, and is obviously a nonlinear system.
Extended reading:How to distinguish between linear and nonlinear _ linear and nonlinear (linear analysis, linear model)
Vacuum UV Curing Machine,Vacuum Curing Machine,UV Machine
Shenzhen Jianjiantong Technology Co., Ltd. , https://www.jjthydrogelprotector.com